Lesson 10: Potentials

10.1 The infinite potential well – 10.2 The finite potential well – 10.3 Simulation programs – 10.4 Progress check – 10.5.Summary

The main topic of this chapter is the solution to the Schrödinger equation in a few simple, special cases, but ones which exhibit typical quantum mechanical phenomena. In addition, several programs for quantum mechanics are introduced.

If you have not yet done so, please now download Chapter 10 of the teaching materials as a pdf file.

10.1 The infinite potential well

The Schrödinger equation was introduced in Section 8.8 as the fundamental equation of quantum mechanics. To find physical states of electrons mathematically, we have to solve the Schrödinger equation.

An exact solution is unfortunately possible only in very rare cases. And this possibility occurs even less frequently with the mathematical tools available in schools. Some of these cases are discussed in this chapter.

On the following pages, we deal with one of the most common examples: Electrons “confined” in a potential well. We then introduce software with which the states of electrons in more complicated potentials can be discussed, at least numerically.

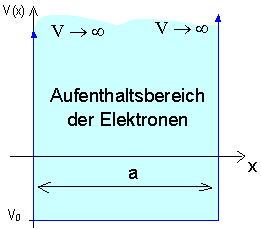
As a first example in which electrons are confined to a limited spatial region, we consider the one-dimensional potential well with infinitely high walls.

A new effect of quantum mechanics appears here:

“Confined” electrons can only assume very specific (quantized) energy values.

The potential profile in the diagram shows: An electron is confined to a spatial region of width a from which it cannot escape. The walls of the potential well form an infinitely high barrier; the potential there approaches infinity. No forces shall act on the electrons inside the potential, which has the constant value $V_0$ there. $V_0$ was thus not set to zero because this will later turn out to be useful in Chapter 13.

With this very simple potential, we can describe quite realistic systems by way of approximation, e. g. quantum dots and quantum wires.

Quantum objects which are limited to a specific spatial region by a potential are said to be bound.

In the interior of the potential well, the Schrödinger equation applies:

$\frac{d^2}{dx^2} \psi_{(x)} = - \frac{2m}{\hbar^2}(E_{ges}-V_0) \cdot \psi_{(x)}$

By rearranging we obtain:

In regions where the potential is infinitely high, the wave function disappears. (The reason for this will be provided in more detail in the next section.) The wave function must therefore fulfill both of the following boundary conditions:

for $x = 0$ : $\psi_{(0)} = 0$ and
for $x = a$ : $\psi_{(a)} = 0$ .

We are therefore looking for a function which reproduces itself after being differentiated twice apart from proportionality factors and which fulfills the two boundary conditions. An approach to finding a solution is therefore $\psi_{(x)} = A sin (B \cdot x)$ , where $A$ and $B$ are constants yet to be determined.

The function fulfills the Schrödinger equation if

$\frac{\hbar}{2m}B^2+V_0 = E_{(ges)} \hspace{35pt} (1)$

as can immediately be verified by inserting it into the equation. The constant $B$ must fulfill a further condition because of the second boundary condition

$B = \frac{\pi \cdot n}{a} \hspace{35pt} f\"ur \: n=1,2,3,\dots$

With Equation (1) it follows that the energy can only assume specific, discrete values:

$E_n = \frac{\hbar^2 \pi^2}{2ma^2} \cdot n^2 + V_0 \hspace{35pt} (n=1,2,3,\dots).$

The possible energy values are identified by the quantum number $n$ . A very specific value of $E$ belongs to each value of $n$ .

The energy of electrons in a potential well of width $a$ with infinitely high walls is quantized. It can only assume the values

$E_n = \frac{\hbar^2 \pi^2}{2ma^2} \cdot n^2 + V_0 \hspace{35pt} (n=1,2,3,\dots)$

which are identified by the quantum number $n$ .

If we insert the values of $B$ into the wave function, this yields solutions which correspond to those of a string which is clamped at both ends.

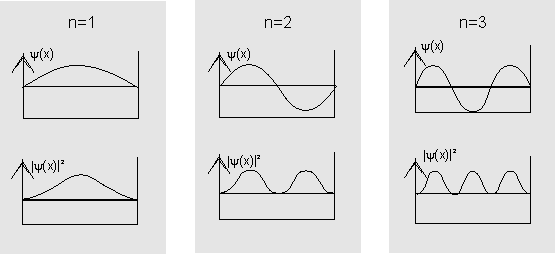
The diagram shows the wave functions (top) and probability densities (bottom) for the first three states in the potential well.

The wave function for electrons in an infinitely deep potential well is:

$\psi_n(x) = A \cdot sin \left( \frac{n \pi}{a}x \right).$

The constant $A$ has still to be determined. It results from the requirement that the sum over all relative incidences has to have the value 1. For a continuous distribution function, we integrate the probability density $|\psi(x)|^2$ over the total width of the potential well (normalization, cf. Chapter 9.1):

$\int_a^0 |\psi(x)|^2 dx =1.$

The stationary states of electrons in an infinite potential well of width a are described by the following wave functions:

$\psi_n(x) = \sqrt{\frac{2}{a}}sin \left( \frac{n \pi}{a}x \right) \hspace{35pt} (n=1,2,3,\dots).$

The three-dimensional potential well is discussed in Chapter 12.1.

Connection to chemistry.

Here you can download an article “Der Potentialtopf als Illustration des quantenmechanischen Eigenschaftsbegriffs” (The potential well as an illustration of the quantum mechanical concept of property)

10.2 The finite potential well

In the last section, we stipulated that the value of the wave function be zero at and beyond the potential wall. In classical terms, this is completely correct, but in quantum mechanical terms, this is only correct in the case of infinitely high walls. To explain this, we now consider the finite potential well and the transition to the limiting case of the potential well with infinitely high walls. One reason for this is that the finite potential well occurs in nature much more frequently than does a well with infinitely high walls.

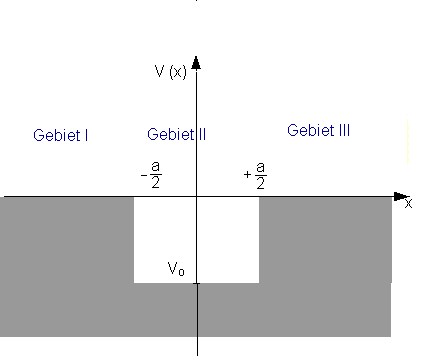
$V_{(x)} = \left\lbrace \begin{array}{cc} 0 \hspace{15pt} f\"ur \: |x| > \frac{a}{2} \hspace{25pt} region \: I + III \\ V_0 \hspace{9pt} f\"ur \: |x| \le \frac{a}{2} \hspace{49pt} region \: II \end{array}$

The Schrödinger equation for the individual regions is:

$f\"ur |x| > \frac{a}{2} \left( \frac{d^2}{dx^2}- \gamma^2 \right) \psi(x)=0 \hspace{35pt} mit \: \gamma^2 = \frac{2m}{\hbar^2}(V_0-E)$

$f\"ur |x| \le \frac{a}{2} \left( \frac{d^2}{dx^2}- k^2 \right) \psi(x)=0 \hspace{65pt} mit \: k^2 = \frac{2mE}{\hbar^2}.$

For simplicity, we only consider solutions which are symmetric about $x = 0$ (positive parity). Then we only need to discuss the region $x > 0$ and can derive the complete solution from the condition $\psi(- x) = \psi(x)$ .

A quite similar calculation can be carried out for antisymmetric solutions (negative parity). We can finally obtain the general solution to the problem by superimposing symmetric and antisymmetric solutions.

In region II, the solution which has positive parity is $\psi_{II}(x) = B \: cos \: kx$ .
In region III, the exponentially decreasing solution of the Schrödinger equation is given by $\psi_{III}(x) = C \: exp(- g x)$ .

The possible values of k (and thus the energy) are determined by the continuity conditions. The values can usually not be given by an explicit expression.

The wave function has the following form:

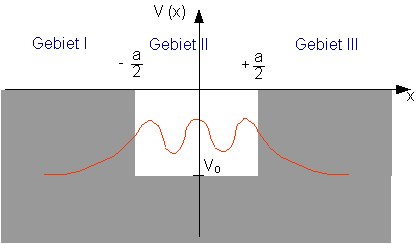
In regions I and III the wave function decreases exponentially in accordance with $\psi_{I/III}(x) = C \: exp(-g |x|)$ .

For $V_0 \gg E$ becomes $\gamma^2=\frac{2m}{\hbar^2}(V_0-E)$ very large. The wave function therefore decreases very rapidly in this case.

In the limiting case $V_0\rightarrow \infty \psi_I$ and $\psi_{III}$ become zero at the edges of the potential well. This is the condition which we had imposed for the infinite potential well.

Another special case is $E = V_0$ . The particles are allowed to stay in region II, in classical physics as well, but have zero kinetic energy there: They are therefore at rest!

The corresponding wave function represents the quantum mechanical situation. Note that the wave function in region $II$ levels out at the maximum value of the cosine wave. – It appears to be a reflection at the free end.

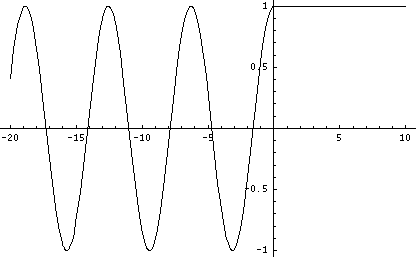
When the particle energy $E$ is greater than the potential step $V_0$ , the mathematical treatment is simplest when we study a wave function entering region I. Part of it is reflected and the other portion will propagate in region II.

The wave function cannot be properly stated in real terms here. We will therefore forego a more detailed treatment of the exact solution. A complex solution can be found in every standard textbook.

10.3 Simulation programs

Program by J. Küblbeck

Program author: Dr. J. Küblbeck, Ludwigsburg

The programs are designed so that pupils can autonomously understand the course content using the simulation programs.

Schrödinger’s snake

This is a program which you can use to work out the energy spectra of the well and the Coulomb potential and the harmonic oscillator yourself by adjusting the $\psi$ function.

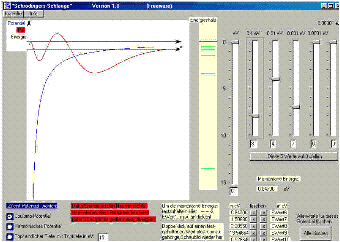
The “Schrödinger’s snake” program is intended for physics teachers who have introduced their pupils to the time-independent real Schrödinger equation in order to calculate energy spectra in a well, harmonic or Coulomb potential with it. The program solves the Schrödinger equation for one electron. Its energy can be so finely adjusted with the aid of slider controls that the $\psi$ function remains bounded. This gives the energy eigenvalues. When the pupils determine the energy eigenvalues themselves with “Schrödinger’s snake”, they find out how extraordinarily precisely these eigenvalues are determined by the Schrödinger equation with its boundary conditions.

Here you can download Schrödinger’s snake as an executable EXE-file.

Schrödinger’s seesaw

With the aid of “Schrödinger’s seesaw”, you can show by means of a simple example what effect the slope of the potential in the time-independent Schrödinger equation has on its solutions and thus on the probability distribution.

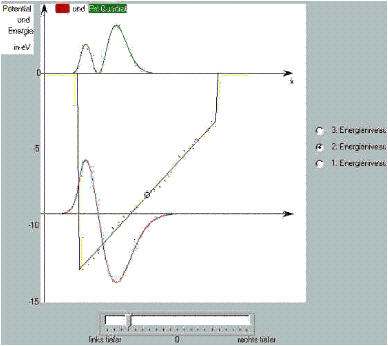
To this end, the bottom of a well potential can be tilted over a large range of angles with a simple slider control.

You can see: In the regions where the difference between energy and potential is large, the second derivative, i. e. the curvature of the $\psi$ function, becomes large and vice versa.

If we consider the potential well to be the zero-order approximation of the Coulomb problem, the sloping well is a good 1st order approximation, which already demonstrates the essential characteristics of the solutions of the Coulomb potential.

Here you can download Schrödinger’s seesaw as an executable EXE file.

10.4 Progress check

The following points were important in this chapter:

Approach to and solution of the Schrödinger equation for the potential well with infinitely high walls.
Energy quantization.
Approach to and solution of the Schrödinger equation for the potential well with infinitely high walls as the motivation for the requirements for continuity.
Transition from the finite to the infinite potential well.

Before you move on to the next chapter, make sure you know the fundamental ideas behind these points. You can then check this with the aid of the Summary.

10.5 Summary

This chapter focused on the application of the Schrödinger equation to two simple examples.

First an example often discussed in lessons was dealt with: The potential well with infinitely high walls. The potential confines the quantum particles to a specific spatial region. A new effect of quantum mechanics appears here: The energies of the particles are quantized.

To provide a motivation for setting the boundary conditions, the next step was to briefly present the finite potential well, and use it to consider the transition to the limiting case of the potential well with infinitely high walls. walls.