10. Potentiale

Lektion 10: Potentiale

10.1 Der unendlich hohe Potentialtopf – 10.2 Der endlich hohe Potentialtopf – 10.3 Simulationsprogramme – 10.4 Selbstkontrolle – 10.5.Zusammenfassung

Der Schwerpunkt dieses Kapitels ist die Lösung der Schrödinger-Gleichung in einigen einfachen Spezialfällen, die aber typische quantenmechanische Phänomene aufzeigen. Zusätzlich werden einige Programme zur Quantenmechanik vorgestellt.

Falls noch nicht geschehen, laden Sie bitte jetzt das Kapitel 10 des Lehrtextes als pdf-Datei herunter.

10.1 Der unendlich hohe Potentialtopf

In Abschnitt 8.8 wurde die Schrödinger-Gleichung als Grundgleichung der Quantenmechanik eingeführt. Um auf mathematischem Wege physikalische Zustände von Elektronen zu finden, müssen wir die Schrödinger-Gleichung lösen.

Leider ist dies nur in den seltensten Fällen exakt möglich. Und noch seltener kann man das mit den mathematischen Mitteln, die in der Schule zur Verfügung stehen. Einige dieser Fälle werden in diesem Kapitel diskutiert.

Auf den folgenden Seiten wird eines der verbreitetsten Beispiele behandelt: in einem Potentialtopf „eingesperrte“ Elektronen. Im Anschluss daran stellen wir Software vor, mit der die Zustände von Elektronen in komplizierteren Potentialen wenigstens numerisch diskutiert werden können.

Als ein erstes Beispiel, in dem Elektronen auf einen begrenzten Raumbereich beschränkt werden, betachten wir den eindimensionalen Potentialtopf mit unendlich hohen Wänden.

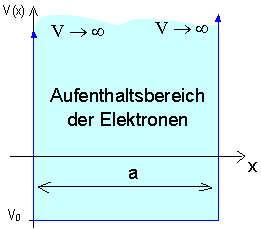
Hier zeigt sich ein neuer Effekt der Quantenmechanik:

„Eingesperrte“ Elektronen können nur ganz bestimmte (quantisierte) Energiewerte annehmen.

Der Potentialverlauf in der Abbildung zeigt: Ein Elektron ist in einem Raumbereich der Breite a eingesperrt, aus dem es nicht entkommen kann. Die Wände des Potentialtopfs bilden eine unendlich hohe Barriere; das Potential geht dort gegen unendlich. Im Inneren des Potentials sollen auf die Elektronen keine Kräfte wirken, dort hat das Potential den konstanten Wert $V_0$ . $V_0$ wurde deshalb nicht Null gesetzt, weil sich dies später in Kapitel 13 als nützlich erweisen wird.

Mit diesem sehr einfachen Potential kann man näherungsweise durchaus realistische Systeme beschreiben, z. B. Quantenpunkte und Quantendrähte.

Quantenobjekte, die durch ein Potential auf einen bestimmten Raumbereich eingeschränkt sind, nennt man gebunden.

Im Inneren des Potentialtopfs gilt die Schrödinger-Gleichung:

$\left[ - \frac{\hbar^2}{2m} \frac{d^2}{d x^2}+V_0 \right] \psi_{(x)} = E_{ges} \cdot \psi_{(x)}.$

Durch Umformung erhält man:

$\frac{d^2}{dx^2} \psi_{(x)} = - \frac{2m}{\hbar^2}(E_{ges}-V_0) \cdot \psi_{(x)}$

In den Bereichen, in denen das Potential unendlich groß ist, verschwindet die Wellenfunktion. (Dies wird im nächsten Abschnitt noch ausführlicher begründet werden.) Die Wellenfunktion muss also die beiden folgenden Randbedingungen erfüllen:

für $x = 0$ : $\psi_{(0)} = 0$ und
für $x = a$ : $\psi_{(a)} = 0$ .

Gesucht ist demnach eine Funktion, die durch zweimaliges Ableiten bis auf Proportionalitätsfaktoren wieder in sich selbst übergeht und die beiden Randbedingungen erfüllt. Dies liefert der Ansatz $\psi_{(x)} = A sin (B \cdot x)$ , wobei $A$ und $B$ noch zu bestimmende Konstanten sind.

Die Funktion erfüllt die Schrödinger-Gleichung, wenn

$\frac{\hbar}{2m}B^2+V_0 = E_{(ges)} \hspace{35pt} (1)$

wie man durch Einsetzen sofort nachrechnen kann. Die Konstante $B$ muss wegen der zweiten Randbedingung noch eine weitere Bedingung

$B = \frac{\pi \cdot n}{a} \hspace{35pt} f\"ur \: n=1,2,3,\dots$

erfüllen. Mit Gleichung $(1)$ folgt, dass die Energie nur bestimmte, diskrete Werte annehmen kann:

$E_n = \frac{\hbar^2 \pi^2}{2ma^2} \cdot n^2 + V_0 \hspace{35pt} (n=1,2,3,\dots).$

Die möglichen Energiewerte werden durch die Quantenzahl $n$ gekennzeichnet. Zu jedem Wert von $n$ gehört ein ganz bestimmter Wert von $E$ .

Die Energie von Elektronen in einem Potentialtopf der Breite $a$ mit unendlich hohen Wänden ist quantisiert. Sie kann nur die Werte

$E_n = \frac{\hbar^2 \pi^2}{2ma^2} \cdot n^2 + V_0 \hspace{35pt} (n=1,2,3,\dots)$

annehmen, die durch die Quantenzahl $n$ gekennzeichnet werden.

Setzt man die Werte von $B$ in die Wellenfunktion ein, ergeben sich Lösungen, die denen einer eingespannten Saite entsprechen.

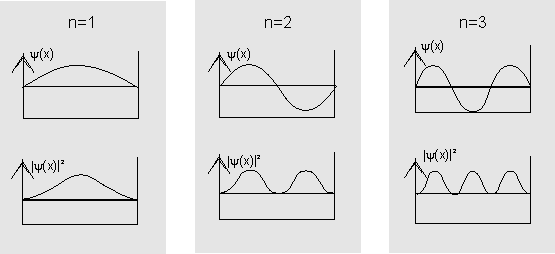
Die Abbildung zeigt die Wellenfunktionen (oben) und die Wahrscheinlichkeitsdichten (unten) der ersten drei Zustände im Potentialtopf.

Die Wellenfunktion für Elektronen im unendlich tiefen Potentialtopf lautet

$\psi_n(x) = A \cdot sin \left( \frac{n \pi}{a}x \right).$

Die Konstante $A$ muss noch bestimmt werden. Sie ergibt sich aus der Forderung, dass die Summe über alle relativen Häufigkeiten den Wert 1 haben muss. Bei einer kontinuierlichen Verteilungsfunktion integriert man über die Wahrscheinlichkeitsdichte $|\psi(x)|^2$ über die gesamte Breite des Potentialtopfs (Normierung, vgl. Kapitel 9.1):

$\int_a^0 |\psi(x)|^2 dx =1.$

Die stationären Zustände von Elektronen in einem unendlich hohen Potentialtopf der Breite a werden durch folgende Wellenfunktionen beschrieben:

$\psi_n(x) = \sqrt{\frac{2}{a}}sin \left( \frac{n \pi}{a}x \right) \hspace{35pt} (n=1,2,3,\dots).$

Der dreidimensionale Potentialtopf wird in Kapitel 12.1 behandelt.

Verbindung zur Chemie.

Hier können Sie sich einen Artikel „Der Potentialtopf als Illustration des quantenmechanischen Eigenschaftsbegriffs“ herunterladen.

10.2 Der endlich hohe Potentialtopf

Im vorangegangenen Abschnitt ist für die Wellenfunktion der Wert Null außerhalb und an der Potentialwand gefordert worden. Dies ist klassisch betrachtet völlig richtig, doch quantenmechanisch stimmt das nur im Fall von unendlich hohen Wänden. Um dies zu erläutern, wird nun der endliche Potentialtopf und der Grenzübergang zum Potential mit unendlich hohen Wänden behandelt. Ein Grund dafür ist, dass dieser in der „Natur“ wesentlich häufiger vorkommt, als ein Topf mit unendlich hohen Wänden.

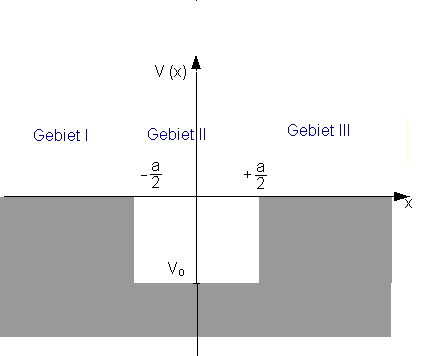
$V_{(x)} = \left\lbrace \begin{array}{cc} 0 \hspace{15pt} f\"ur \: |x| > \frac{a}{2} \hspace{25pt} Gebiet \: I + III \\ V_0 \hspace{9pt} f\"ur \: |x| \le \frac{a}{2} \hspace{49pt} Gebiet \: II \end{array}$

Die Schrödinger-Gleichung lautet für die einzelnen Gebiete:

$f\"ur |x| > \frac{a}{2} \left( \frac{d^2}{dx^2}- \gamma^2 \right) \psi(x)=0 \hspace{35pt} mit \: \gamma^2 = \frac{2m}{\hbar^2}(V_0-E)$

$f\"ur |x| \le \frac{a}{2} \left( \frac{d^2}{dx^2}- k^2 \right) \psi(x)=0 \hspace{65pt} mit \: k^2 = \frac{2mE}{\hbar^2}.$

Der Einfachheit halber betrachten wir nur Lösungen, die symmetrisch um $x = 0$ sind (positive Parität). Dann müssen wir nur den Bereich $x > 0$ diskutieren und können die vollständige Lösung aus der Bedingung $\psi(- x) = \psi(x)$ gewinnen.

Eine ganz analoge Rechnung ließe sich für antisymmetrische Lösungen (negative Parität) durchführen. Durch Überlagerung von symmetrischen und antisymmetrischen Lösungen kann man schließlich die allgemeine Lösung des Problems gewinnen.

In Gebiet II ist die Lösung positiver Parität $\psi_{II}(x) = B \: cos \: kx$ .
In Gebiet III ist die exponentiell abfallende Lösung der Schrödinger-Gleichung durch $\psi_{III}(x) = C \: exp(- g x)$ gegeben.

Die möglichen Werte von $k$ (und damit der Energie) werden durch die Stetigkeitsbedingungen bestimmt. Die Werte können in der Regel nicht durch eine explizite Formel angegeben werden.

Die Wellenfunktion hat die folgende Gestalt:

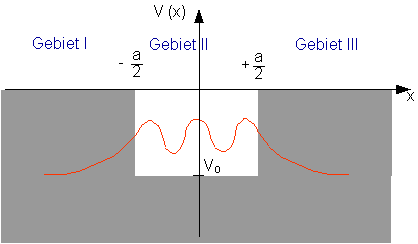
In Gebiet I und III fällt die Wellenfunktion gemäß $\psi_{I/III}(x) = C \: exp(-g |x|)$ exponentiell ab.

Für $V_0 \gg E$ wird $\gamma^2=\frac{2m}{\hbar^2}(V_0-E)$ sehr groß. Die Wellenfunktion fällt daher in diesem Fall sehr schnell ab.

Im Grenzfall $V_0\rightarrow \infty$ werden $\psi_I$ und $\psi_{III}$ an den Rändern des Potentialtopfs gleich Null. Dies ist die Bedingung, die wir beim unendlich hohen Potentialtopf angesetzt hatten.

Ein anderer Sonderfall ist $E = V_0$ . Die Teilchen dürfen sich auch klassisch in dem Bereich $II$ aufhalten, haben dort aber die kinetische Energie Null: Sie ruhen also!

Die entsprechende Wellenfunktion gibt die quantenmechanische Situation wieder. Zu beachten ist, dass die Wellenfunktion im Gebiet II das Maximum der Kosinuswelle konstant fortsetzt. – Es scheint eine Reflexion am losen Ende zu sein.

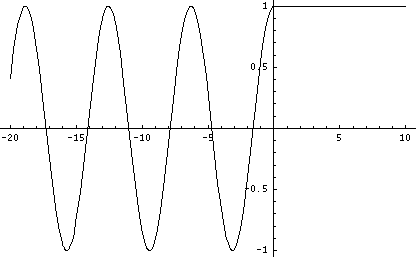
Wenn die Teilchenenergie $E$ größer als die Potentialstufe $V_0$ ist, dann ist die mathematische Behandlung am einfachsten, wenn man eine im Gebiet I einlaufende Wellenfunktion untersucht. Sie wird zum einen Teil reflektiert und wird sich zum anderen Teil im Gebiet II ausbreiten.

Die Wellenfunktion lässt sich hier nicht sauber reell formulieren. Deshalb wird auf eine genauere Behandlung der exakten Lösung verzichtet. Eine komplexe Lösung findet sich in jedem Standardlehrbuch.

10.3 Simulationsprogramme

Programme von J. Küblbeck

Programmautor: Dr. J. Küblbeck, LudwigsburgDie Programme sind darauf ausgerichtet, dass Schüler mit den Simulationsprogrammen selbstständig die Lerninhalte erfassen können.

Schrödingers Schlange
Dies ist ein Programm, mit dem man sich die Energiespektren von Topf- und Coulomb-Potential sowie harmonischem Oszillator durch Anpassen der $\psi$ -Funktion selbst erarbeiten kann.

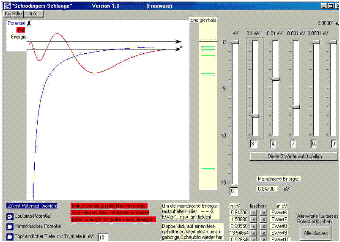
Das Programm „Schrödingers Schlange“ ist für Physiklehrerinnen und -lehrer gedacht, die mit ihren Schülerinnen und Schülern die zeitunabhängige, reelle Schrödinger-Gleichung eingeführt haben, um damit die Energiespektren in Topf-, harmonischem oder Coulomb-Potential zu berechnen. Das Programm löst die Schrödinger-Gleichung für ein Elektron. Mit Hilfe von Reglern kann dessen Energie so fein eingestellt werden, dass die $\psi$ -Funktion beschränkt bleibt. Dies liefert die Energieeigenwerte. Wenn die Schüler selbst mit „Schrödingers Schlange“ die Energieeigenwerte bestimmen, erfahren sie, wie außerordentlich scharf diese durch die Schrödingergleichung mit ihren Randbedingungen bestimmt sind.

Hier können Sie sich Schrödingers Schlange als ausführbare EXE-Datei herunterladen.

Schrödingers Wippe

Mit Hilfe von „Schrödingers Wippe“ kann man an einem einfachen Beispiel zeigen, wie sich die Neigung des Potentials in der zeitunabhängigen Schrödinger-Gleichung auf deren Lösungen und damit auf die Wahrscheinlichkeitsverteilung auswirkt.

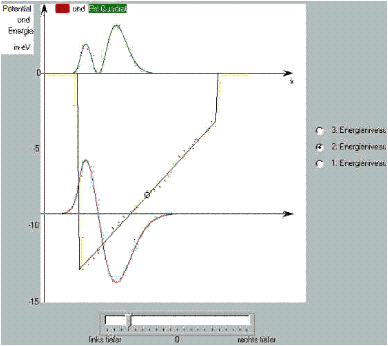
Zu diesem Zweck kann man mit einem einfachen Regler den Boden eines Topfpotentials in einem weiten Bereich kippen.

Man sieht: In Bereichen in denen die Differenz zwischen Energie und Potential groß ist, wird auch die zweite Ableitung, also die Gekrümmtheit der $\psi$ -Funktion groß und umgekehrt.

Wenn man den Potentialtopf als nullte Näherung des Coulomb-Problems ansieht, ist der schiefe Topf eine gute 1. Näherung, die bereits die wesentlichen Charakteristika der Lösungen des Coulombpotentials zeigt.

Hier haben Sie die Möglichkeit, Schrödingers Wippe als ausführbare EXE-Datei herunterzuladen.

10.4 Selbstkontrolle

In diesem Kapitel waren die folgenden Inhalte von Bedeutung:

Ansatz und Lösung der Schrödinger-Gleichung für den Potentialtopf mit unendlich hohen Wänden.
Quantisierung der Energie.
Ansatz und Lösung der Schrödinger-Gleichung für den Potentialtopf mit endlich hohen Wänden zur Motivation der Stetigkeitsforderungen.
Übergang vom endlich zum unendlich hohen Potentialtopf.

Bevor Sie zum nächsten Kapitel weitergehen, vergewissern Sie sich, dass Sie über die Grundzüge dieser Inhalte Bescheid wissen. Anschließend können Sie dies anhand der Zusammenfassung überprüfen.

10.5 Zusammenfassung

In diesem Kapitel stand die Anwendung der Schrödinger-Gleichung an zwei einfachen Beispielen im Vordergrund.

Zunächst wurde ein im Unterricht oft besprochenes Beispiel der Potentialtopf mit unendlich hohen Wänden behandelt. Die Quantenteilchen sind durch das Potential auf einen bestimmten Raumbereich eingesperrt. Hier zeigt sich ein neuer Effekt der Quantenmechanik: die Energien der Teilchen sind gequantelt.

Um die Randbedingungen zu motivieren, wurde als nächstes der endliche Potentialtopf kurz vorgestellt und an diesem der Grenzübergang zum Potentialtopf mit unendlich hohen Wänden betrachtet.