3.1 Light in the interferometer – 3.2 Light beam to photons – 3.3 Interferometry – 3.4 Path of a photon? – 3.5 Explanation of the result – 3.6 Does the photon split up?
3.7 Progress check – 3.8 Summary
This lesson investigates the behavior of individual photons in an interferometer. The light here exhibits wave and particle properties in the same experiment. This is one example for an important aspect of quantum mechanics: The “duality” of wave and particle. We will see that the behavior of light cannot be explained by a pure particle or a pure wave model.
The objective of this lesson is to gain an initial insight into this strange quantum behavior using the example of a special experiment. One of the later lessons (Probability interpretation and wave function, Lesson 5.5) strives to provide a more detailed understanding of this strange behavior. It will be seen there how the “mystery of duality” is solved by Born’s probabilistic interpretation.
Misconceptions about wave-particle duality
We now come to one of the most astonishing results of the whole course. The question is whether the property “path” can be assigned to a photon in the interferometer: May we imagine that a certain photon reaches the screen on precisely one of two possible paths? In the “Interferometer” simulation program we obtain results which allow only one conclusion: A photon does not have the property “path”.A further experiment shows that the photon does not split up between the two paths either. This is the first time we reach a point where our classical concepts fail.
If you have not done so already, please now download Chapter 3 of the teaching materials as a pdf file.
User information
In this chapter, several experiments are conducted with the aid of the Interferometer simulation program. Please download the Interferometer.exe program.
How do I download the “Interferometer” simulation program?
- Click on the underlined “Interferometer.exe” link (see above).
- Save this file on your computer.
- Open the “Interferometer.exe” simulation program from wherever you have saved it.
- Open the simulation program by clicking the “Start” button. Minimize its window so that the Windows taskbar is visible. You can now switch backwards and forwards between the teaching materials in the Internet and the “Interferometer” simulation program.
3.1 Light in the interferometer
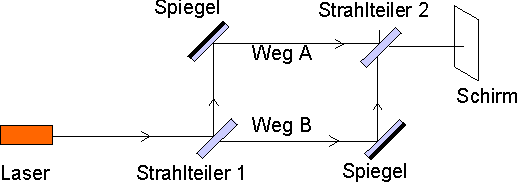
The illustration shows the set-up of a Mach-Zehnder interferometer. When the light of a laser is incident on a beam splitter (semi-transparent mirror), it is split up into two partial beams. These partial beams travel along different paths, path A and path B. Two mirrors in the paths A and B deflect each part of the laser light through 90° and a further beam splitter at their point of intersection “mixes” them again. An interference pattern, which is classically caused by the difference in path lengths which result from the different routes taken from the source to the screen, is obtained on the screen.
This experiment can be conducted with the aid of the “Interferometer” simulation program.
Experiment 3.1:
How is the interference pattern produced?
3.2 From beam of light to individual photons
If several neutral density filters are placed in front of a laser in a very dark room, the light intensity is attenuated so much that nothing can be seen with the naked eye. The light is now “diluted” so much that it consists of individual photons, which can only be detected with the aid of a CCD element.
Experiment 3.2:
3.3 Interferometry with individual photons
We can now use the “Interferometer” simulation program to conduct the interference experiment in the Mach-Zehnder interferometer which we considered above with individual photons by selecting “individual photons” as the light source.
Experiment 3.3: Each photon triggers only one individual detector pixel on the CCD element. The distribution which results when only a small number of photons are detected seems to exhibit no regularity at all.
What happens when a large number of photons have been detected?
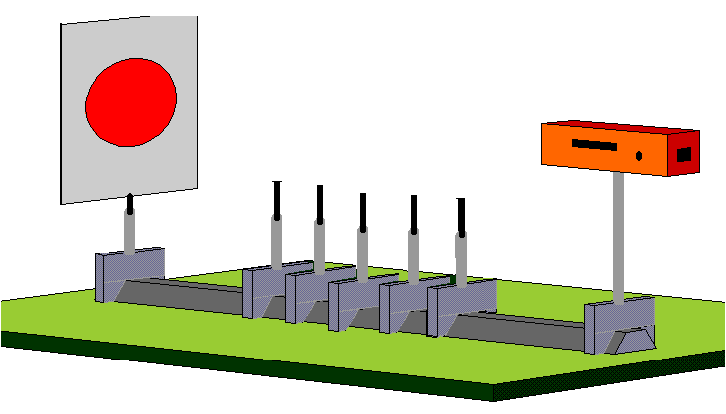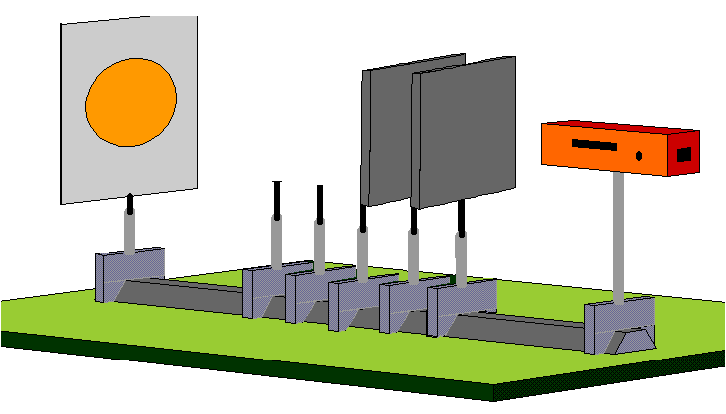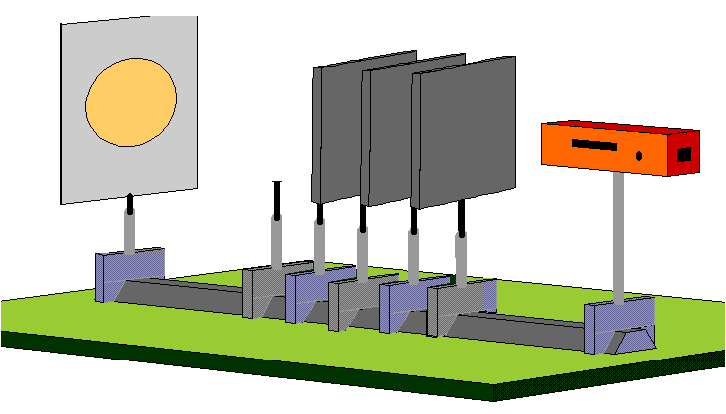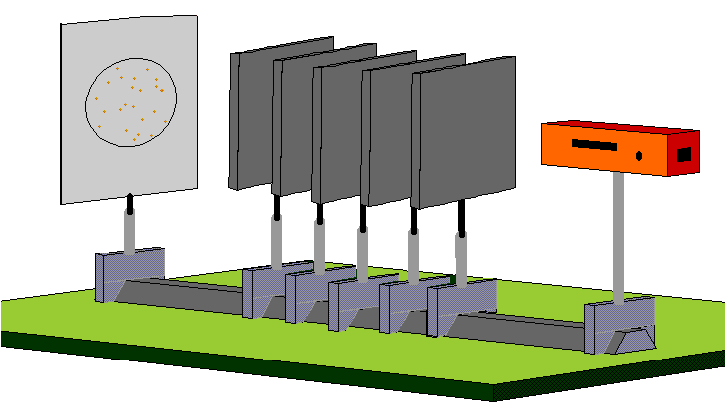
The interference pattern already observed in Experiment 3.1 with high-intensity laser light slowly emerges. The animation shows the gradual build-up of the interference pattern from individual photon “impacts”.
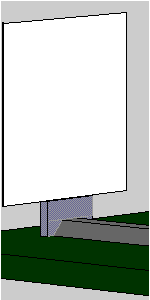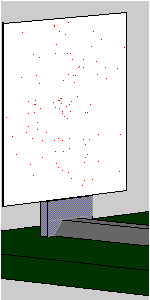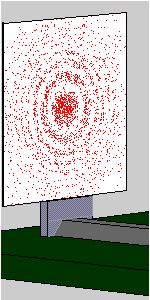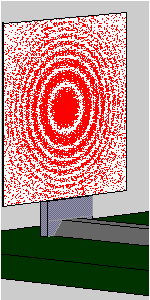
Has such an experiment really been carried out?
The experiment considered is one example for the “duality” of wave and particle for photons. On the one hand, the behavior whereby the interaction takes place in a localized way and an irregular distribution of detected photons is seen initially, is typical for particles. On the other hand, the interference pattern which evolves from a large number of individual photon impacts is a characteristic feature of a wave. This yet again illustrates clearly: A simple alternative between wave and particle does not exist in quantum mechanics.
These results can be summarized as follows:
It is not possible to describe the physical behavior of photons in a pure particle or a pure wave model. A satisfactory explanation must combine characteristics of both models.
If we consider a series of experiments in which only a single photon is detected in each case, and which are so far apart in time that a mutual influence can be excluded, we will have a surprising result:
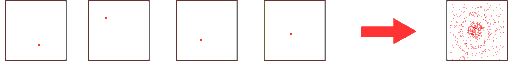
Each experiment provides only one single spot, which certainly cannot be considered to be a wave phenomenon or an attenuated interference image. All the independent experiments taken together provide the interference pattern typical for waves, however.This experiment clearly shows that the interference pattern cannot be attributed to an interaction of the photons with each other, no matter what kind of interaction it may be.
3.4 Can a path be assigned to a photon?
Can we imagine that a photon can be localized inside the interferometer? Or in other words: Does a photon have the property “path” inside the interferometer?
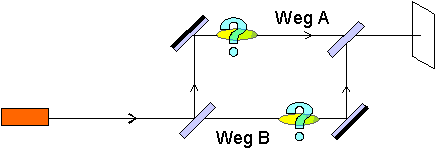
If this were the case, each individual photon must have taken either path A or path B to the detector in the illustration above (i.e. taking only one of the two paths).
To clarify this, we use the concept of dynamic property which was introduced in the Preparation lesson (see also Summary of Lesson 2).
If every photon in the interferometer is labeled such that a decision on the path is possible, we can get to the bottom of the question as to whether a photon has the property “path” in the interferometer. We now want to use the already familiar property of polarization to label the photons.
To this end we first consider a preparatory experiment:
Experiment 3.4:
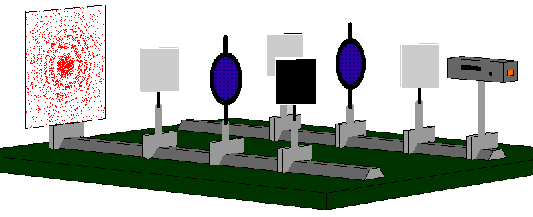
Inserting the two polarization filters with the same setting does not change anything in respect of the result of Experiment 3.3. The interference pattern emerges gradually, but slightly more slowly, since the polarization filters absorb half of the photons on average.Neither does the result change with the polarization filters set to horizontal.
When the polarization filter in path B is set to horizontal and the polarization filter in path A is set to vertical, we label the two paths A and B using the two polarization filters. By measuring the direction of polarization, we can now decide for each individual photon whether it has taken path A (polarization filter A) or path B (polarization filter B). The property “path” is thus labeled here by the polarization.
Experiment 3.5:
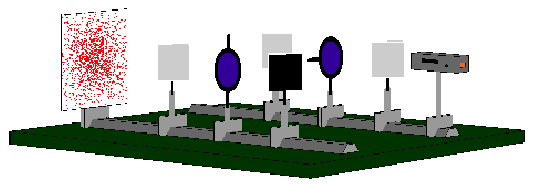
The photons registered in this experiment do not produce an interference pattern, but a distribution without any structure. The animation shows the gradual emergence of this distribution.
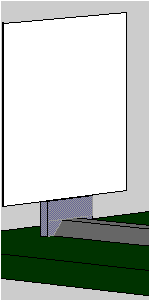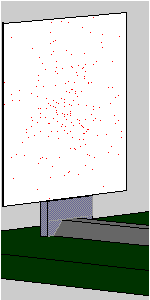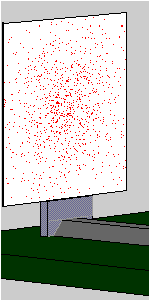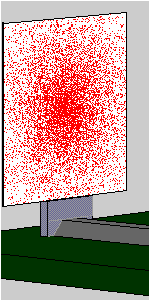
Does the same not happen with laser light?
Comparing Experiments 3.4 and 3.5 leads to the following result:
In quantum mechanics it is possible that a specific, classically well-defined property (e.g. “path A” or “path B”) cannot be ascribed to a quantum object.
Can the path information be erased again?
3.5 Graphic explanation of the result
The distributions observed on the screen in Experiments 3.4 and 3.5 differ in the following points:
In the case of the interference pattern, there are regions on the screen in which it is certain that no photon is registered (Experiment 3.4). However, photons are detected in these regions when a structureless distribution can be seen on the screen (Experiment 3.5). In order to decide whether photons are found in the regions in question, the position of both polarization filters must be known.
How can a photon possess this “knowledge”? This is where the concept of the photon as a localized entity that arrives at the screen by taking either path A or path B runs into difficulties.
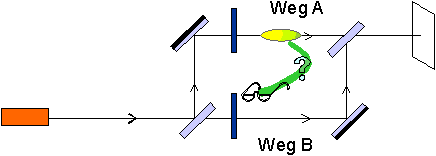
If a concept of action at a distance, as shown in the diagram, is to be avoided, the only conclusion remaining is that our initial assumption was wrong.
A photon cannot be considered as a localized entity with a fixed position; it is not possible to ascribe one of the two paths to this photon.
Here you can download several worksheets.
3.6 Does the photon split up?
We have not yet succeeded in providing a graphic description of how the photons behave in the interferometer. Does the idea that a photon somehow splits up at the first semi-transparent mirror, and that the separate parts of the photon follow different paths to the second semi-transparent mirror, where they recombine, provide a possible explanation? No, because this concept is wrong!
Experiment 3.6:
Two parts of a photon cannot be detected, since only one of the detectors is ever triggered and never both at the same time. In addition, a detector always registers all the energy E = h · f which the individual photons possessed when they left the lamp. This refutes the idea that a photon splits into separate parts.
The experiment of Grangier, Roger and Aspect
Interpretation of this experiment from the point of view of the wave-particle problem
The apparently contradictory results of Experiments 3.5 and 3.6 can be clarified with a more detailed consideration of measurement in quantum mechanics.
Behind the first beam splitter, a photon does not have the property “path” (Experiment 3.5). Even though it does not have this property, precisely one of the possible measured values “path A” or “path B” is always found in a measurement, however (Experiment 3.6).
In general, this finding can be stated as follows:
Although a quantum object does not have to possess a property (e. g. “path in the interferometer”), a specific value is always found when this property is measured (e. g. “path A” or “path B”).
You can download a worksheet here.
3.7 Progress check
The following points were important in this chapter:
How an interferometer is designed and works, and how to use the “Interferometer” simulation program.
Experimental transition from beam of light to individual photons.
Why can quantum objects not be described in a pure particle or a pure wave model?
Can a path be assigned to a photon?
Does the photon split up?
Before you move on to the next chapter, make sure you know the fundamental ideas behind these points. You can then check this with the aid of the Summary.
3.8 Summary of Lesson 3: Waves and particles
The wave property of light can be demonstrated with the aid of an interferometer. The light beam is split into two parts by a beam splitter. The two partial beams are deflected through 90° with the aid of mirrors so that they intersect again. A further beam splitter is positioned at their point of intersection, which “mixes” the two beams again.
If the light of a laser is used as the light beam, an interference pattern can be observed on the screen behind the second beam splitter. What happens if we consider individual photons?
By inserting several neutral density filters into this arrangement, individual photons can be registered on the screen. After some time, the interference pattern produced is the same as is produced when the laser is used without neutral density filters. The experiment shows that it is not possible to describe the behavior of the photons with a pure wave or pure particle model. Furthermore, it turned out in the computer simulation that there are experiments where it is impossible to assign a specific property, such as the path, to a quantum object.
The idea that a photon splits up to explain the behavior of the photons in the interferometer, was refuted.
But: Although it is possible that a photon (or more generally a quantum object) does not possess a property, a specific value will always be found in a measurement.