4.1 Double-slit experiment with light waves – 4.2 The double-slit experiment with individual photons and the probabilistic statements of quantum theory
4.3 Preparation and probabilistic statements 4.4 Progress check – 4.5 Summary
In this lesson, we will take a first look at the probabilistic interpretation of quantum mechanics. We will consider the behavior of individual photons at the double slit and come up against the fact that quantum objects have to be described statistically. Since it is unfortunately very difficult to investigate individual photons in a real experiment, we will use a simulation program for the double-slit experiment.
In addition, a number of concepts will be introduced (e. g. the concept of a statistical ensemble) which will later turn out to be useful.
If you have not done so already, please download Chapter 4 of the teaching materials as a pdf file.
User information
In the following chapters, the double-slit simulation program is used on a frequent basis. Please download the Doppelspalt.exe program.
How do I download the “double slit” simulation program?
- Click on the underlined “Doppelspalt.exe” link.
- Save the Doppelspalt.exe into any directory.
- Open the Doppelspalt.exe program and minimize its window so that the Windows taskbar is visible. You can now switch backwards and forwards between the teaching materials in the Internet and the “double slit” simulation program.
4.1 Double-slit experiment with light waves
When the light of a laser is incident on a double slit in a darkened room, the following pattern can be seen:

The pattern observed is explained in classical optics by the fact that elementary waves originate from both slits and interfere with each other.
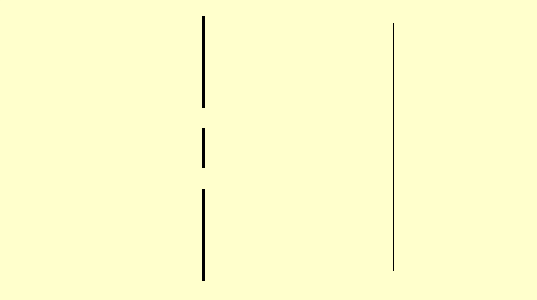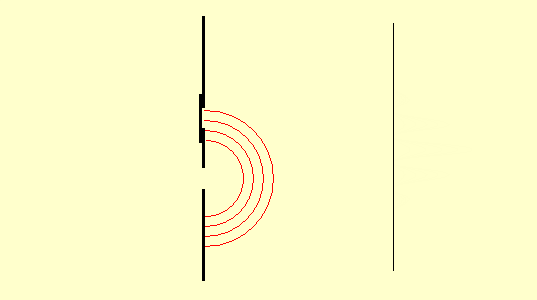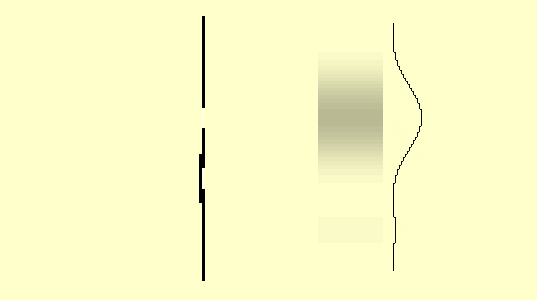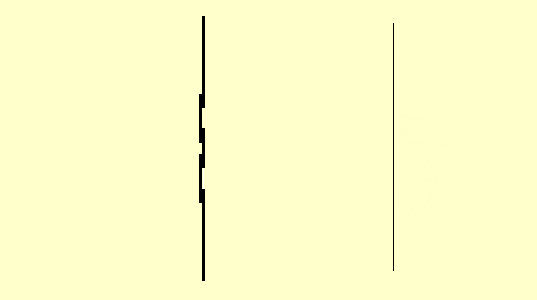
The wave behavior of light can be recognized from interference phenomena
4.2 The double-slit experiment with individual photons and the probabilistic statements of quantum theory
Start the simulation program for the double-slit experiment and carry out Experiments 4.2 – 4.4 described in Section 4.2 of the teaching materials.
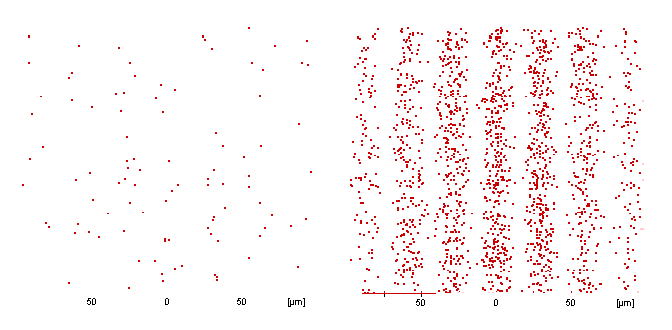
After the photon source is switched on in the simulation, individual photons are detected on the screen (cf.top left-hand picture) as point-like “spots”. The distribution here seems to be completely random. A pattern which corresponds to the well-known double-slit interference pattern with waves (cf. Section 4.1) emerges only gradually after a large number of photons have impinged.
If we were now to stop the experiment and send only a single photon, we could not predict at which position on the screen it would be localized. If we were to allow 100 photons, for example, to impinge, it would certainly be possible to make a relative estimate (probabilistic statement) of the point of impact.
The results of the experiments can be summarized as follows:
It is not possible to predict an individual event (precise specification of the impact point of a photon), and we are instead forced to move to statistical statements (distribution of many photons).
4.3 Preparation and probabilistic statements
In classical mechanics, identically prepared (same speed, same angle etc.), but different throws of a basketball, for example, would always lead to the same point of impact, the basket, for instance. The results are reproducible.
Even if quantum objects, such as photons in the double-slit experiment, are identically prepared (same energy, same emission from the source), it is not possible here to predict the result of the measurement for an individual photon – in contrast to classical mechanics, individual results are not reproducible.
The relative incidence of the photons detected at a specific position (their statistical distribution) can be predicted, however, since a reproducible distribution on the screen results downstream of the interaction with the double slit after the experiment has been carried out on a large number of identically prepared photons.
In this context it is useful to introduce the concept of the ensemble. An ensemble is very large number of objects prepared in the same way which have no mutual influence.
The behavior of ensembles of quantum objects is therefore governed by probabilistic statements. Individual events cannot be predicted, however. Intuitively and classically one doubts that where a photon impinges is left to chance, and it could be argued that hidden parameters or properties have possibly been overlooked in the preparation. If we could find all these characteristics, it would accordingly be possible to accurately predict the impact point of an individual photon. But according to quantum mechanics, this is precisely the point – there is no characteristic and there are no additional parameters – a “more complete” preparation of the photons is not possible. Instead, statistical statements about the relative incidence of the results for frequent repetitions of the same experiment can be made. This is a characteristic of quantum mechanics.
This probabilistic interpretation of quantum mechanics will be reinforced in the next lesson, Lesson 5 “Electrons as quantum objects”. It deals with how quantitative, probabilistic predictions can be made with the wave function.
Is it really the case that no statements about individual events are possible in quantum mechanics?
Here you can download worksheets by J. Küblbeck.
4.4 Progress check
The following points were important in this chapter:
How to use the double-slit simulation program.
What does an ensemble of quantum objects mean?
Which predictions about the impact point of the photons on the screen are possible with the double-slit experiment?
Before you move on to the next chapter, make sure you know the fundamental ideas behind these points. You can then check this with the aid of the Summary.
4.5 Summary
Instead of an interferometer, we now use the double-slit experiment for the interference experiments. As we did in Lesson 3, we now move from a beam of light to individual photons.
It is impossible to predict where an individual photon will impinge. If we consider large numbers of photons, however, a more precise prediction is possible.
Quantum mechanics provides statistical statements about the relative incidence of the results when the same experiment is repeated many times. These statistical statements are reproducible.
An ensemble is a very large number of objects prepared in the same way which have no mutual influence.
