12.1 Was sind Atome? – 12.2 Linienspektren – 12.3 Das Bohrsche Atommodell – 12.4 Abschied vom Bohrschen Atommodell
12.5 Quantisierung der Energie im Franck-Hertz-Versuch – 12.6 Dreidimensionaler Potentialtopf und Orbitale – 12.7 Selbstkontrolle – 12.8 Zusammenfassung
Bisher sind nur Quantenobjekte wie Elektronen oder Photonen betrachtet worden. In diesem Kapitel soll das Atom behandelt werden. Dabei stehen das Bohrsche Atommodell, die Quantisierung der Energie und der dreidimensionale Potentialtopf im Vordergrund.
Falls Sie es noch nicht gemacht haben, laden Sie sich bitte jetzt das Kapitel 12 des Lehrtextes als pdf-Datei herunter.
12.1 Was sind Atome?
Der Name Atom (= unteilbar) stammt aus der Zeit, in der die Atome als die kleinsten Materiebausteine angesehen wurden.
Die moderne Physik hat jedoch gezeigt, dass Atome aus einem sehr kleinen, positiv geladenen Atomkern und an diesen gebundene Elektronen besteht. Sie sind also keine elementaren Bausteine.
12.2 Linienspektren
Betrachtet man das Licht verschiedener Leuchtstoffröhren oder einer Quecksilberdampflampe mit Hilfe eines Spektroskops, beobachtet man statt des gewohnten kontinuierlichen Spektrums z.B. einer Glühlampe, nur einzelne Linien in bestimmten Farben (Experiment 12.1). Ein solches Spektrum nennt man diskretes oder Linienspektrum.

Diese Spektren konnten im 19.Jahrhundert nicht erklärt werden. Die Bemühungen, eine Erklärung zu finden, bedeuteten einen Anstoß in der Entwicklung der Quantenmechanik.
Balmer fand 1885 eine mathematische Gesetzmäßigkeit auf der Grundlage der beim atomaren Wasserstoff beobachteten Linien, die noch weitere, bis dahin nicht beobachtete Linien vorhersagte:
Die Spektrallinien von atomaren Wasserstoff werden durch die folgende Formel (Balmer-Formel) beschrieben:
![]()
Dabei ist ![]() eine Konstante, die sogenannte Rydberg-Frequenz. Die Zahl m klassifiziert die verschiedenen Serien des Wasserstoffs:
eine Konstante, die sogenannte Rydberg-Frequenz. Die Zahl m klassifiziert die verschiedenen Serien des Wasserstoffs:
![]() Lyman-Serie im Ultravioletten
Lyman-Serie im Ultravioletten
![]() Balmer-Serie teilweise im Sichtbaren
Balmer-Serie teilweise im Sichtbaren
![]() Paschen-Serie im Infraroten
Paschen-Serie im Infraroten
![]() Brackett-Serie im Infraroten.
Brackett-Serie im Infraroten.
![]() ist eine natürliche Zahl, (mit
ist eine natürliche Zahl, (mit ![]() ), die die Linien innerhalb einer Serie kennzeichnet.
), die die Linien innerhalb einer Serie kennzeichnet.
12.3 Das Bohrsche Atommodell
1913 stellte Niels Bohr ein Atommodell auf, das auch noch heute als weitverbreitete Modellvorstellung dient. Dieses Modell von Bohr war ein sehr wichtiger Zwischenschritt auf dem Weg zum heutigen Verständnis der Atome und man konnte damit erstmals ein Linienspektrum beschreiben. Manche Annahmen von ihm erwiesen sich bis heute als gültig:
Der Drehimpuls ![]() ist ein Vielfaches von
ist ein Vielfaches von ![]() . Damit ist auch die Energie in Atomen quantisiert. Die Elektronen im Atom können nur in Zuständen mit ganz bestimmten Werten ihrer Energie existieren (den sogenannten stationären Zuständen).
. Damit ist auch die Energie in Atomen quantisiert. Die Elektronen im Atom können nur in Zuständen mit ganz bestimmten Werten ihrer Energie existieren (den sogenannten stationären Zuständen).
Ein Atom strahlt nur dann ein Photon ab, wenn ein Elektron von einem stationären Zustand mit der Energie ![]() in einen anderen Zustand mit einer niedrigeren Energie
in einen anderen Zustand mit einer niedrigeren Energie ![]() übergeht. Für die Frequenz des abgestrahlten Photons gilt:
übergeht. Für die Frequenz des abgestrahlten Photons gilt:
![]()
12.4 Abschied vom Bohrschen Atommodell
Mit der Entwicklung der Quantentheorie zeigte sich, dass das Bohrsche Atommodell mit den Annahmen von 1913 nicht richtig war. Bohrs Modell bedeutete schon einen Bruch mit den Gesetzen der klassischen Physik (ad-hoc-Postulat nur bestimmter zulässiger Bahnen, strahlungsloser Umlauf). Doch es zeigte sich, dass noch grundlegendere Veränderungen notwendig waren, z. B.
- Die Elektronen kreisen nicht auf wohldefinierten Bahnen um den Kern, d.h. man kann ihnen keinen Ort zuschreiben (siehe Doppelspaltversuche in Kapitel 6).
Diese Aussage lässt sich mit der Heisenbergschen Unschärferelation begründen. Die mittlere kinetische Energie auf Bahnen lokalisierter Elektronen übersteigt demnach die zur Ionisierung nötige Energie von ![]() um ein Vielfaches. Das Atom würde sofort ionisiert werden und damit zerstört.
um ein Vielfaches. Das Atom würde sofort ionisiert werden und damit zerstört.
Ist das Bohrsche Atommodell noch zeitgemäß?
12.5 Quantisierung der Energie im Franck-Hertz-Versuch
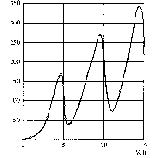
Ein Versuch, der die von Bohr ad hoc formulierte Quantisierung der Energie stützt, ist der Franck-Hertz-Versuch (Experiment 12.3). Der Versuch zeigt, dass Quecksilberatome nur einen ganz bestimmten Energiebetrag aufnehmen können.
12.6 Dreidimensionaler Potentialtopf und Orbitale
In der Quantenmechanik muss die Quantisierung der Energie nicht wie bei Bohr postuliert werden, sondern sie ergibt sich auf natürliche Weise aus der Theorie (vgl. Kapitel 10).
Es lässt sich eine Analogie zwischen einem Elektron im Wasserstoffatom und einem Elektron in einem Potentialtopf finden: Beide Elektronen sind „eingesperrt“, d. h. sie sind durch Kräfte an einen bestimmten Raumbereich gebunden.
In erster Näherung können wir also den unendlich hohen Potentialtopf als „Modell-Atom“ betrachten, allerdings nun im dreidimensionalen Raum.
Die eindimensionale Schrödinger-Gleichung für den unendlich hohen Potentialtopf lautet:
![]()
Die Erweiterung auf den dreidimensionalen Fall ist recht einfach: Da alle drei Koordinaten gleichberechtigt sind, gilt:
![]() . Somit ist der Operator der kinetischen Energie:
. Somit ist der Operator der kinetischen Energie:
![]()
und die Schrödinger-Gleichung lautet:
![]()
Da das Potential im Inneren des Topfes konstant ist, ist der zweckmäßige Lösungsansatz das Produkt der Lösungen für eindimensionale Potentialtöpfe:
![]()
Einsetzen dieses Ansatzes in die Schrödinger-Gleichung liefert:
![Rendered by QuickLaTeX.com \[ \left[ - \frac{\hbar^2}{2m}\left( \frac{n^2_x \pi^2}{a^2} - \frac{n^2_y \pi^2}{a^2} - \frac{n^2_z \pi^2}{a^2} \right) \right] \psi_{n_xn_yn_z}(x,y,z) = E_{ges} \cdot \psi_{n_xn_yn_z}(x,y,z) \]](https://www.milq.info/wp-content/ql-cache/quicklatex.com-ccda86a45bd23aa85fd886b963d4e7e0_l3.png)
Mit
![]()
ist die Schrödinger-Gleichung erfüllt.
Damit haben wir eine Wellenfunktion und die möglichen Energien für den dreidimensionalen Potentialtopf gefunden.
Deutung:
Anstatt einer Quantenzahl treten nun drei Quantenzahlen ![]() ,
, ![]() und
und ![]() auf. Da diese drei unabhängig voneinander alle möglichen Werte annehmen können, entsteht eine große Anzahl von Möglichkeiten. Um die Übergänge graphisch zu veranschaulichen, trägt man die Energieniveaus in ein Termschema ein.
auf. Da diese drei unabhängig voneinander alle möglichen Werte annehmen können, entsteht eine große Anzahl von Möglichkeiten. Um die Übergänge graphisch zu veranschaulichen, trägt man die Energieniveaus in ein Termschema ein.
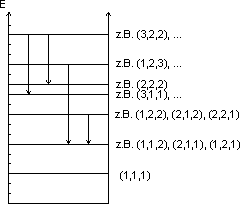
Der Grundzustand ist mit der Quantenzahlkombination ![]() gegeben. In der Abbildung (a) ist die Wahrscheinlichkeitsdichte für diesen dargestellt.
gegeben. In der Abbildung (a) ist die Wahrscheinlichkeitsdichte für diesen dargestellt.

Es gibt drei Zustände für den nächsten höheren Energieeigenwert, die gegeben sind durch die Quantenzahlkombinationen
* ![]() (Abbildung (b))
(Abbildung (b))
* ![]() (Abbildung (c))
(Abbildung (c))
* ![]() (Abbildung (d)).
(Abbildung (d)).
Alle drei Zustände (b) – (d) besitzen die gleiche Energie.
Die Wahrscheinlichkeitsverteilungen können für verschiedene Werte der Quantenzahlen dargestellt werden. Sie entsprechen den aus der Chemie bekannten Orbitalen. Damit werden die Raumbereiche beschrieben, in denen die Wahrscheinlichkeit ein Elektron zu treffen, besonders hoch ist.
Aufenthaltwahrscheinlichkeit bei antiprotonischem Wasserstoff.
12.7 Selbstkontrolle
In diesem Kapitel waren die folgenden Inhalte von Bedeutung:
- Linienspektrum leuchtender Gase.
- Bohrsches Atommodell (Quantisierung der Energie, Frequenz der abgestrahlten Photonen).
- Was muss am Bohrschen Atommodell revidiert werden?
- Franck-Hertz-Versuch.
- Problemstellung und Lösung des dreidimensionalen Potentialtopfs mit der Schrödinger-Gleichung.
Bevor Sie zum nächsten Kapitel weitergehen, vergewissern Sie sich, dass Sie über die Grundzüge dieser Inhalte Bescheid wissen. Anschließend können Sie dies anhand der Zusammenfassung überprüfen.
12.8 Zusammenfassung von Kapitel 12: Atome
Neben den kontinuierlichen Spektren beobachtet man Linienspektren (oder auch diskrete Spektren) z.B. bei leuchtenden Gasen. Diese lassen sich nur mit Hilfe der Quantenmechanik erklären.
Die bis heute von Bohr in seinem Atommodell formulierten gültigen Aussagen sind:
- die Quantisierung der Energie, die auch mit dem Franck-Hertz-Versuch gestützt wird,
- die Frequenz abgestrahlter Photonen beim Übergang der Energiezustände
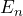 in
in 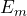 beträgt:
beträgt:
![]()
Die Vorstellung von wohldefinierten Umlaufbahnen der Elektronen um den Atomkern kann nicht aufrecht erhalten werden, da dies der Heisenbergschen Unbestimmtheitsrelatin widerspricht.
Der im Kapitel 10 angesprochene, einfache Potentialtopf wird ins Dreidimensionale erweitert. Dieses Modell des dreidimensionalen Potentialtopfs kann als eine Vorstufe des Atoms angesehen werden. Aus der Behandlung des Potentialtopfs ergibt sich eine natürliche Erklärung für das Vorhandensein der Orbitalen eines Atoms.
