13. Das Wasserstoff-Atom

13.1 Energiewerte des Wasserstoff-Atoms durch Kastenpotential-Näherung – 13.2 Ermitteln der Potentialtopf-Breite – 13.3 Ermitteln der Potentialtopf-Tiefe
13.4 Bestimmen der Energiewerte – 13.5 Selbstkontrolle – 13.6 Zusammenfassung

In dieser Lektion wird ein Standardproblem der Quantenphysik behandelt: das Wasserstoff-Atom. Sie werden eine Methode kennenlernen, mit der sich die Energieniveaus näherungsweise mit Schulmitteln berechnen lassen. Dazu wird das Coulomb-Potential des Kerns durch ein geeignet angepasstes Kastenpotential ersetzt.¹ Diese Methode besitzt den Vorteil, dass alle Näherungen bereits im klassischen Potential vorgenommen werden. Die anschließende quantenmechanische Rechnung ist dann exakt.

Falls Sie es noch nicht gemacht haben, laden Sie sich bitte jetzt das Kapitel 13 des Lehrtextes als pdf-Datei herunter.

13.1 Energiewerte des Wasserstoff-Atoms durch Kastenpotential-Näherung

Beim Wasserstoffatom hält sich ein einzelnes Elektron im Coulomb-Potential des Atomkerns auf. Es kann dabei nicht beliebige Werte der Gesamtenergie annehmen; seine Energie ist quantisiert. Die Diskussion der Energiequantisierung im Wasserstoffatom nimmt eine zentrale Stellung im Atomphysik-Unterricht ein.

Die Quantenmechanische Berechnung der Energieniveaus des Wasserstoff-Atoms kann in der Schule nicht durchgeführt werden. Man ist auf vereinfachte Modelle und Näherungen angewiesen. Am verbreitetsten ist der Rückgriff auf das Bohrsche Atommodell Übersicht über in Schulbüchern gebräuchliche Zugänge zum Wasserstoff-Atom).

Allerdings: Setzt man als Ziel des Quantenphysik-Unterrichts die Abkehr von klassischen Denkweisen, ist die Verwendung des Bohrschen Atommodells problematisch, denn dort laufen die Elektronen wie in der klassischen Physik auf wohldefinierten Bahnen. Man muss auf Begriffe zurückgreifen, die in der Quantenmechanik keine Berechtigung mehr haben (Orte und Bahnen von Elektronen), wodurch klassischen Fehlvorstellungen der Schülerinnen und Schüler Vorschub geleistet wird.

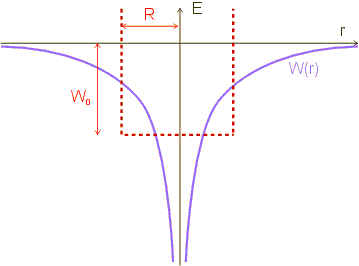
Das Coulomb-Potential des Atomkerns wird durch ein „ähnliches“ Potential ersetzt: durch ein Kastenpotential mit unendlich hohen Potentialwänden. Genauer gesagt handelt es sich um einen dreidimensionalen, kastenförmigen Potentialtopf mit der Breite $2R$ und der Energiedifferenz $W_0$ zwischen dem „Boden“ des Potentialtopfs und dem Energienullpunkt. Für die Breite und die Energiedifferenz müssen Werte gefunden werden, so dass der Potentialtopf das Coulombpotential möglichst gut approximiert.

13.2 Ermitteln der Potentialtopf-Breite

In der klassischen Physik kann sich ein gebundenes Elektron (Energie $E$ $R$ nicht eindringen, denn sonst wäre seine potentielle Energie größer als seine Gesamtenergie.

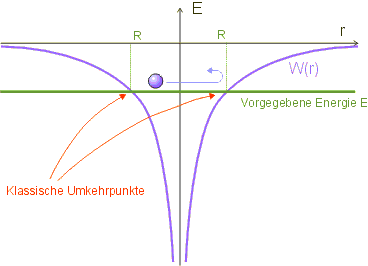
Der Umkehrpunkt ist demnach dadurch gekennzeichnet, dass die kinetische Energie Null ist; die gesamte Energie $E_{ges}$ ist dann gleich der potentiellen Energie:

$E_{ges}=−e24\pi\epsilon_0R$

bzw. nach $R$ aufgelöst:

$R=−e24\pi\epsilon_0E_{ges}$

Der maximale Abstand $R$ hängt also von der Energie $E_{ges}$ ab.

Damit hat man eine klassische Abschätzung für den Bereich gewonnen, innerhalb dessen sich das Elektron aufhält. Das Coulomb-Potential wird in unserem Modell durch einen Potentialtopf der Breite $2R$ ersetzt; innerhalb dieses Bereichs wird das Potential als konstant angenommen, der Außenbereich ist für das Elektron unzugänglich (unendlich hohe Potentialwände).

13.3 Ermitteln der Potentialtopf-Tiefe

Möchte man dieses Problem anschaulich und ohne die bei der etwas exakteren Mittelung des Coulomb-Potentials über eine Kugel mit Radius $R$ immer noch nötige Mathematik lösen, geht man wie folgt vor:

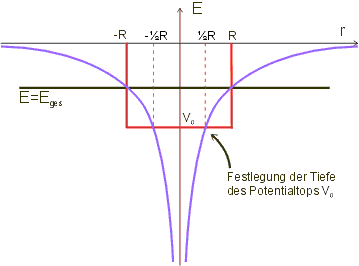
Wie man aus der Abbildung ersehen kann, verläuft das Potential für $r < R$ immer unterhalb der horizontalen Linie bei der Gesamtenergie $E_{ges}$ . Der Wert von $W_0$ muss also unterhalb von $E_ {ges}$ liegen. Eine einfache Abschätzung erhält man, wenn man festlegt, dass $W_0$ den Wert des Coulomb-Potentials an der Stelle $r =\frac{1}{2} R$ hat (Abbildung). Es gilt demnach (Einsetzen der Formel für $R$ (siehe oben):

$W_0 = W\left(r=\frac{1}{2}R\right) = W \left(r=-\frac{1}{2}\frac{e^2}{4\pi\epsilon_0E}\right)$

Mit dem expliziten Ausdruck für das Coulomb-Potential $W$ ergibt dies:

$W_0=\frac{e^2}{4\pi\epsilon_0} \cdot 2 \cdot \frac{4\pi\epsilon_0E}{e^2}$

und das Endergebnis für $W_0$ lautet:

$W= 2 \cdot E_{ges} = -2 \cdot |E_{ges}|.$

Potentielles Verständnisproblem beim Anpassen des Energienullpunkts.

13.4 Bestimmen der Energiewerte

Das klassische Modellpotential, das das Coulombpotential gut approximiert, ist durch die bisherigen Ergebnisse festgelegt. Die Parameter des dreidimensionalen, unendlich hohen Potentialtopfs wurden zu

$W_0=2 \cdot E_{ges}$

und

$R = \frac{e^2}{4 \pi \epsilon_0 |E_{ges}|} \hspace{35pt} (1)$

bestimmt.

Nun kann man mit der quantenmechanischen Berechnung der Energiewerte fortfahren.
Die Energieniveaus beim dreidimensionalen Potentialtopf sind bereits bekannt:

$E_{ges} = \frac{\hbar^2 \pi^2}{2m(2R)^2} \cdot (n^2_x + n^2_y + n^2_z) + W_0 \hspace{35pt} (2),$

mit der Elektronenmasse m und den Quantenzahlen $n_x, n_y, n_z$ . Wir beschränken uns auf Zustände, die keine Raumrichtung auszeichnen. Dann gilt $n_x = n_y = n_z =:n$ , so dass der Elektronenzustand durch eine einzige Quantenzahl $n$ beschrieben wird. Die Energieniveaus aus Gleichung $(2)$ werden dann zu

$E_{ges} = \frac{\hbar^2 \pi^2}{2m(2R)^2} \cdot 3n^2 + W_0 \hspace{35pt} (3).$

Setzt man die vorher bestimmten Parameter $R$ und $W_0$ ein, erhält man:

$E_{ges} = \frac{\hbar^2 \pi^2}{2m} \cdot 3n^2 \cdot \frac{(4 \pi \epsilon_0)^2 E^2_{ges}}{4e^4} +2E_{ges}$

und daraus

$E_{ges} = - \frac{16}{3 \pi^2} \cdot \frac{me^4}{2 \hbar^2 (4 \pi \epsilon_0)^2} \cdot \frac{1}{n^2}$

Dies ist das Endergebnis unserer Modellrechnung zum Wasserstoff-Atom. Vergleicht man mit dem exakten Ergebnis, findet man, dass sich die Energieniveaus bis auf den Faktor $16/3 \pi^2 = 0,54$ korrekt ergeben.

Vor- und Nachteile dieser Methode

¹W. R. Theis, Begründung diskreter Eigenwerte für gebundene Zustände ohne Lösung der Eigenwertgleichung, Physik und Didaktik 22 (3), 198 (1994)

13.5 Selbstkontrolle

In diesem Kapitel waren die folgenden Inhalte von Bedeutung:

Vereinfachung des Wasserstoff-Problems durch Anpassen eines Potentialtopfs mit unendlich hohen Wänden
Energieeigenwerte des Wasserstoff-Potentials.

Bevor Sie zum nächsten Kapitel weitergehen, vergewissern Sie sich, dass Sie über die Grundzüge dieser Inhalte Bescheid wissen. Anschließend können Sie dies anhand der Zusammenfassung überprüfen.

13.6 Zusammenfassung von Kapitel 13: Das Wasserstoff-Atom

In der Schule lässt sich die Schrödinger-Gleichung für das Wasserstoff-Atom nicht exakt lösen. Deshalb wird in diesem Kapitel eine Approximationsmethode vorgestellt, mit der man die $1/n^2$ -Abhängigkeit der Energieeigenwerte gewinnen kann.

Die Grundidee besteht darin, das Coulomb-Potential durch einen geeignet gewählten Potentialtopf mit unendlich hohen Wänden anzunähern. Die klassischen Umkehrpunkte der Bewegung bestimmen die Potentialtreitopfbe.

Man erhält eine selbstkonsistente Gleichung zur Ermittlung der Energieeigenwerte.

Die Methode ist auch für andere Potentiale anwendbar. Bedingung ist, dass die entsprechende klassische Bewegung ebenfalls durch Umkehrpunkte begrenzt ist.