Sichere Kommunikation mittels Quantenphysik

Das Glossar behandelt wichtige Begriffe. Bei unklaren Begriffen darfst du gerne darauf zugreifen:

Überblicksvideo

Lernmaterial

Die Kommunikation ist ein wichtiger Aspekt unseres alltäglichen Lebens. Sie spielte auch in der Geschichte der Menschheit eine bedeutende Rolle, insbesondere die abhörsichere Kommunikation. Die klassische Kryptografie bietet interessante Ansätze an, um dies zu sichern. Im Prinzip sind aber klassische Ansätze fundamental unsicher. Außerdem ist es möglich, dass du belauscht wirst ohne dies zu merken. Die Quantenphysik bietet eine physikalisch abhörsichere Kommunikation, insbesondere eine sichere Verteilung von Verschlüsselungsschlüsseln, an. Mit Verschlüsselungsschlüsseln enkodiert und dekodiert man Nachrichten. Aber wie ist das möglich? Was sind die zugrundeliegenden Phänomene?

Die Quantenphysik bietet zwei essentielle Prinzipien zur Gewährleistung einer sicheren Kommunikation an: das No-Cloning Theorem und das Prinzip der Komplementarität. Das No-Cloning Theorem besagt, dass es nicht möglich ist, den Zustand eines einzelnen Quantenobjekts zu klonen, d.h. eine exakte Kopie davon herzustellen, die in jeder Hinsicht mit dem Original übereinstimmt. Das Prinzip der Komplementarität ist im Grundprinzip 4 folgendermaßen zusammengefasst worden:

Grundprinzip 4: Komplementarität

Es gibt Paare von Observablen, die man nicht gleichzeitig an einem Ensemble von Quantenobjekten auf bestimmte Werte präparieren kann.

Lass uns ein Beispiel betrachten um das Grundprinzip zu veranschaulichen. Alice (Person A) und Bob (Person B) möchten einen Schlüssel über einen sicheren Kanal verteilen. Eine Lauscherin, Eve, hat Zugang zu der Kommunikation bzw. zum Kommunikationskanal.

Die Schlüsselverteilung erfolgt über den Polarisationszustand von einzelnen Photonen. Wir betrachten hierbei zwei Basen mit insgesamt vier Polarisationszuständen. Eine Basis ist die H/V Basis mit horizontal und vertikal polarisierten Photonen, die andere Basis ist die +/- Basis mit +45° und -45° polarisierten Photonen. Alice und Bob wählen ein gemeinsames Codesystem und kodieren bspw. horizontal oder +45° polarisierte Photonen mit einer 1 und vertikal oder -45° polarisierte Photonen mit einer 0. Auf diese Weise werden sie in der Lage sein Bitsequenzen auszutauschen. Um die Schlüsselverteilung zu gewährleisten, müssen Alice und Bob in der gleichen Basis arbeiten. Alice ist die Senderin, Bob der Empfänger. Da Alice die Bitsequenz senden muss, präpariert sie ein Photon in einem bestimmten Zustand – sei dies nun ein horizontal polarisiertes Photon – kündigt dies Bob an und sendet das Photon. Nun misst Bob das Photon in der H/V Basis und misst ein horizontal polarisiertes Photon (der Detektor detektiert das Photon). Gemäß des Codesystems kodiert er dies als eine 1. Auf diese Weise können Alice und Bob Bitsequenzen austauschen und kommunizieren. Alice sendet präparierte Photonen einer bestimmten Polarisation, kündigt dies Bob an und Bob empfängt diese Photonen, misst diese in der richtigen Basis und empfängt die von Alice gewählte Polarisation. Das Photon wird entweder am Detektor detektiert – es wird nicht vom Polarisationsfilter absorbiert – oder das Photon wird nicht am Detektor detektiert – es wird vom Polarisationsfilter absorbiert.

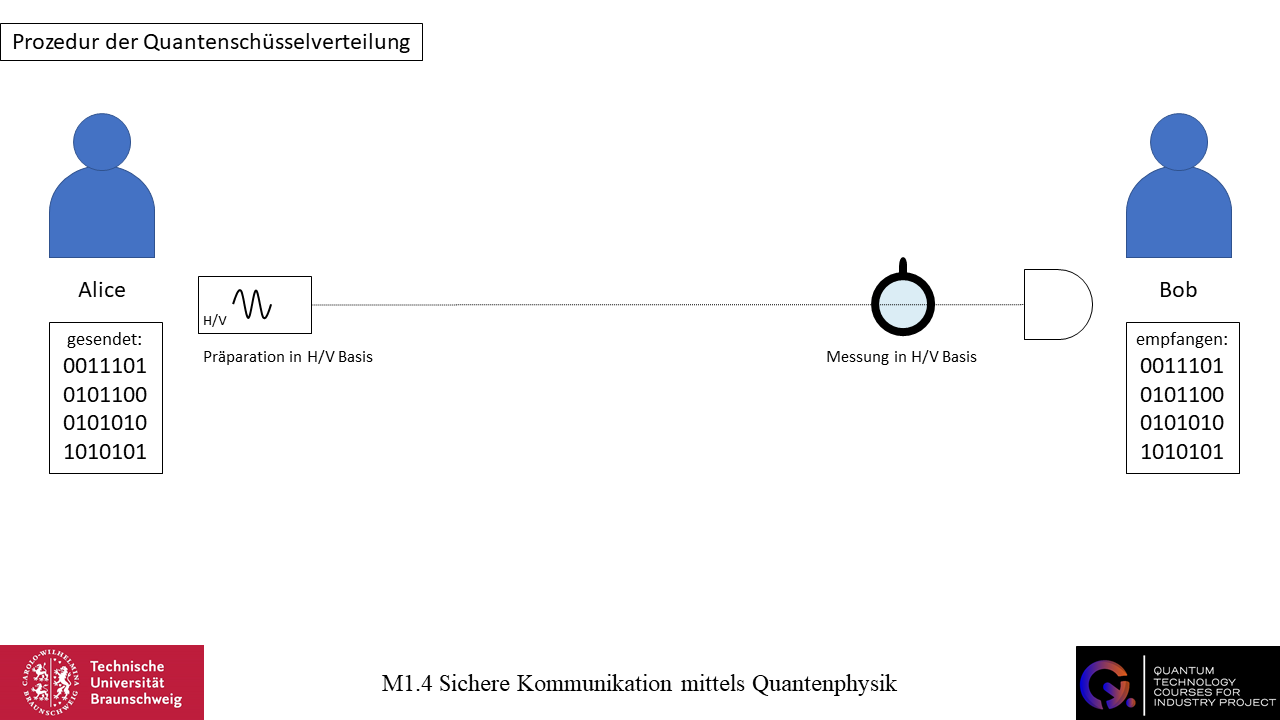
Nun betrachten wir eine dritte Person, Eve. Eve hat Zugriff auf die Kommunikation zwischen Alice und Bob. Eve muss den Zustand des Photons messen um an die Information zu gelangen, die kommuniziert wird. Ein Kopieren des Photons ist nicht möglich (No-Cloning Theorem). Im Gegensatz zum klassischen Lauschangriff ist es im Quanten-Lauschangriff also nicht möglich, die Nachricht unbemerkt zu kopieren. Eve muss den Zustand des „Original“-Photons messen. Hierfür muss sie eine bestimmte Basis wählen in der sie die Messung durchführt.

Wir gehen davon aus, dass Alice und Bob in der gleichen Basis arbeiten. Präpariert Alice demnach ein Photon in der H/V Basis, so misst Bob auch in der H/V Basis. Präpariert Alice ein Photon in der +/- Basis, so misst auch Bob in der +/- Basis. Es ist gerade nicht weiter wichtig, wie genau Alice und Bob dies bewerkstelligen.

Schlussendlich gibt es in diesem Kontext zwei Möglichkeiten: Entweder arbeitet Eve in der gleichen Basis wie Alice und Bob oder Eve arbeitet in der anderen Basis zu Alice und Bob. Wir schauen uns nun beide Szenarien etwas genauer an:

Wenn Eve in der gleichen Basis wie Alice und Bob arbeitet, ist sie in der Lage den Zustand des Photons in der richtigen Basis zu messen. Im Anschluss präpariert sie ein Photon in der gleichen Basis und sendet dieses an Bob. Der Lauschangriff wird nicht bemerkt.

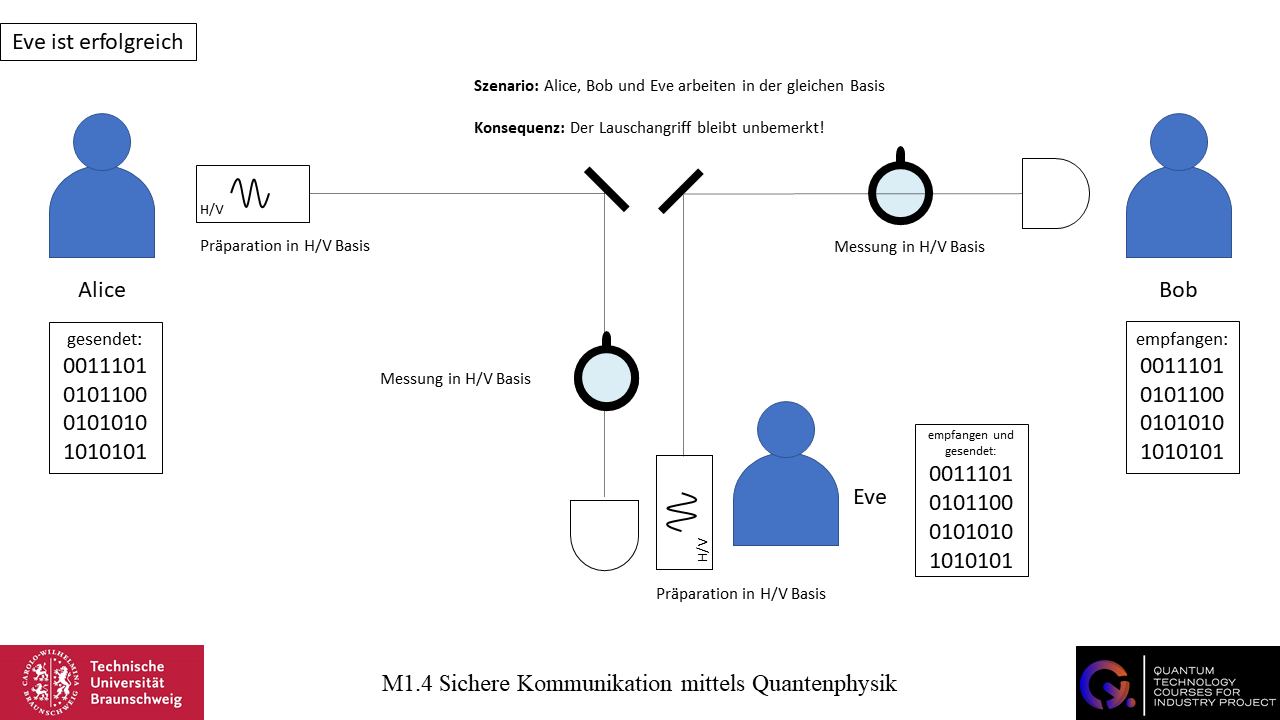
Wenn Eve nicht in der gleichen Basis wie Alice und Bob arbeitet, wird sie aufgrund der Komplementarität auch nicht in der Lage sein die Information des Anfangszustands des Photons zu erhalten. Stattdessen misst sie einen zufälligen Zustand der anderen Basis. Sie sendet ein Photon an Bob, welches in der anderen Basis präpariert ist. Bob misst das Photon und erhält ein zufälliges Ergebnis, welches von Alice’s Anfangszustand abweichen kann. Aber warum geschieht so etwas?

Am Anfang ist das Photon nicht auf einen bestimmten Wert präpariert worden. Alice präpariert das Photon und gibt dem Photon die Eigenschaft eines bestimmten Wertes, bspw. ist das Photon nun horizontal polarisiert. Eine Messung in der H/V Basis würde nun das eindeutige Ergebnis ergeben, dass das Photon horizontal polarisiert ist. Das Prinzip der Komplementarität besagt nun, dass es Paare von Observablen, also beobachtbaren Größen, gibt, die man nicht gleichzeitig auf bestimmte Werte präparieren kann. Die Polarisation in H/V sowie +/- Basis sind Observablen und zudem auch zueinander komplementäre Observablen. Führt man eine Messung in +/- Basis durch, so misst man das Photon hinsichtlich einer, zu ihrer Präparation komplementärer, Polarisationsbasis. Das Photon ist in H/V Basis präpariert, wird aber in +/- Basis gemessen; H/V und +/- sind aber zueinander komplementär. Da das Photon bereits in H/V präpariert ist, kann es nicht gleichzeitig in +/- auf einen bestimmten Wert präpariert sein. Die Messung in +/- Basis liefert folglich zufällige Werte. Damit erhält Eve keine nützliche Information über das von Alice gesendete Bit. Außerdem lässt sich aus dem gemessenen Wert auch nicht der zuvor bestehende Zustand ableiten, die Messung in der komplementären Basis liefert wirklich zufällige Ergebnisse. Eine Analogie zu der Komplementarität ist durch zwei ineinander verwobene Kreise gegeben. Entfernst du einen Kreis, so ist der andere Kreis nicht vollständig und der Umfang des Kreises nicht eindeutig einsehbar.

Wir schauen uns nun unterschiedliche Szenarien an um einen vertieften Einblick zu bekommen und verschiedene Prozesse auszuarbeiten. Nochmals möchten Alice und Bob über Polarisationszustände einzelner Photone kommunizieren und Eve ist eine Lauscherin und hat einen Zugang zu deren Kommunikation. Alice und Bob arbeiten immer in der gleichen Basis, wir gehen nicht näher darauf ein, wie sie dies bewerkstelligen oder wie Alice Bescheid weiß, dass Bob die gleiche Basis verwendet.

Im ersten Szenario ändern Alice und Bob ihre Basen nicht. Somit arbeiten sie immer entweder in der H/V oder der +/- Basis. Eve weiß, dass die Basis nicht geändert wird und arbeitet auch immer in einer Basis. Mit einer Wahrscheinlichkeit von 50% wird Eve die richtige Basis wählen. Falls sie die richtige Basis wählt, wird der Lauschangriff unbemerkt bleiben. Falls sie die falsche Basis wählt, wird sie mit einer Wahrscheinlichkeit von 50% ein zufälliges Ergebnis messen, dass dem richtigen Ergebnis entspricht. Im Anschluss sendet sie ein Photon an Bob. Bob aber misst das Photon in der falschen Basis – in Bezug zu der Basis von Eve – und bekommt auch zufällige Messergebnisse. Unter diesen Rahmenbedingungen unterscheidet sich das Ergebnis von Bob mit einer Wahrscheinlichkeit von 50% von der Bitsequenz, die ursprünglich von Alice verschickt wurde, wir können also folgern, dass in etwa 50% der Bitsequenz von Bob falsch sein wird. Wenn Alice und Bob nun ihre Werte vergleichen, bemerken sie die Lauscherin, Eve.

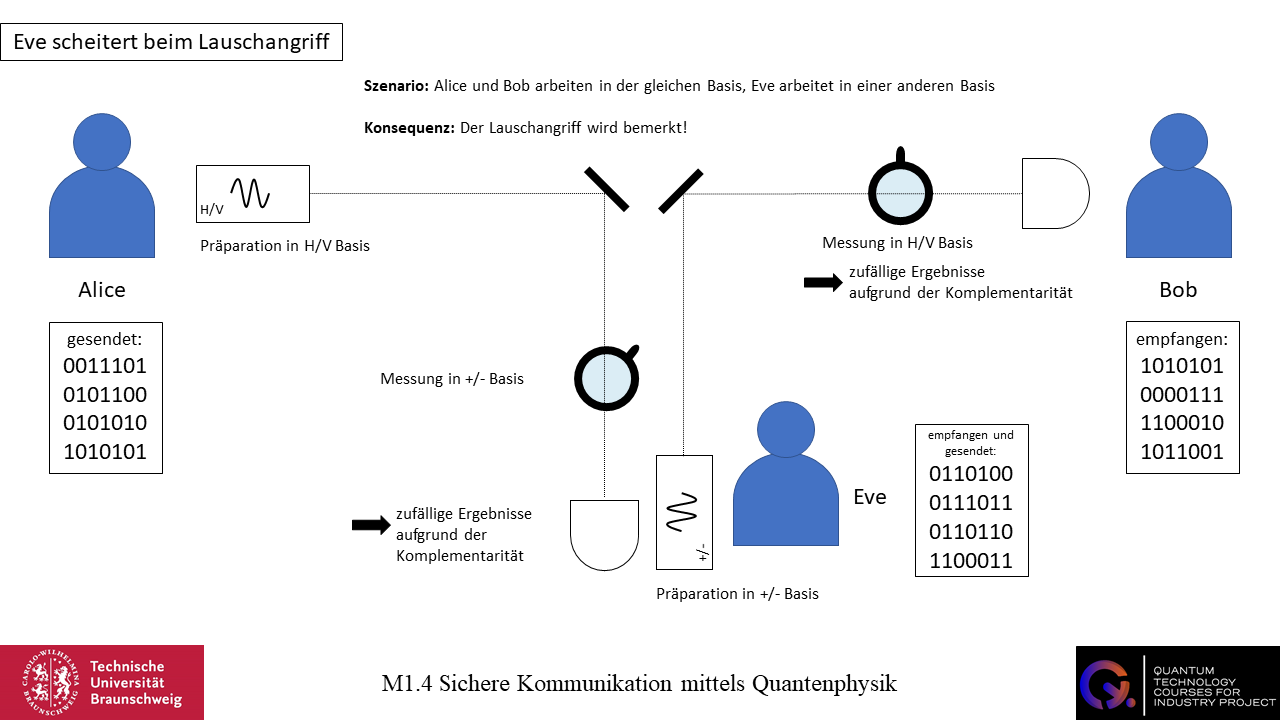
Im zweiten Szenario ändern Alice und Bob ihre Basen nach jedem Bit an Informationen. Demnach können sie nach jedem Bit an Information entweder ihre Basis ändern oder die gleiche Basis beibehalten. Nun macht es keinen Unterschied, ob Eve Bescheid weiß, dass Alice und Bob ihre Basis ändern oder in der gleichen Basis verbleiben. Die Basis von Eve wird zufällig mit der Basis von Alice und Bob übereinstimmen. Die Wahrscheinlichkeit hierfür liegt bei 50%. Falls Eve die richtige Basis hat, bemerken Alice und Bob nichts. Falls Eve die falsche Basis wählt, beträgt die Wahrscheinlichkeit eines fehlerhaften Bits bei Bob 50%. Da die Basis selber nach jedem Bit zufällig gewählt wird, ist die gesamte Nachricht in 25% der Fälle wahrscheinlich falsch und das Abhören wird bemerkt.

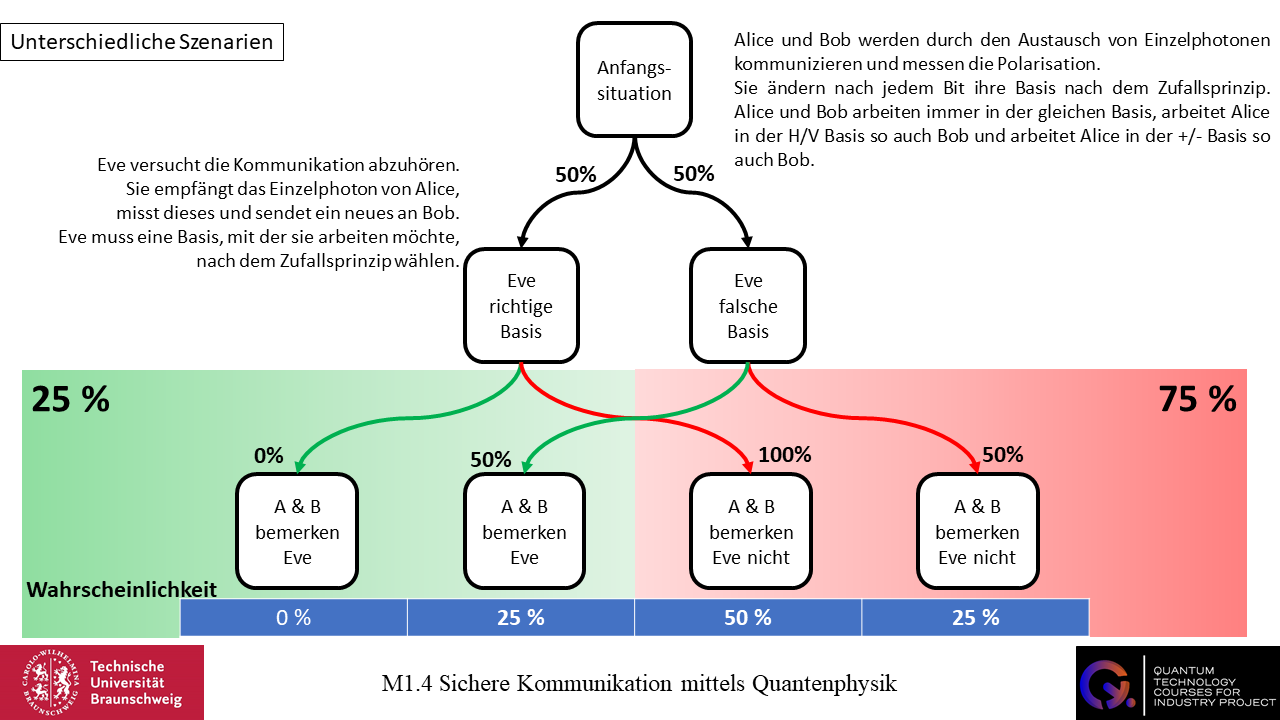
Zusammenfassend lässt sich feststellen, dass das Prinzip der Komplementarität und das No-Cloning Theorem von fundamentaler Bedeutung sind, wenn es um die sichere Verteilung von Verschlüsselungsschlüsseln geht. Auf theoretischer Ebene ermöglicht die Quantenphysik eine physikalisch abhörsichere Kommunikation. Die Anwendung der Theorie jedoch kann sich als schwierig erweisen…

Aufgaben

Aufgabe 1

Benenne das Grundprinzip 4 und erkläre dessen Bedeutung.

Erkläre kurz und prägnant anhand des Beispiels von Alice, Bob und Eve, warum die Quantenschlüsselverteilung theoretisch abhörsicher ist.

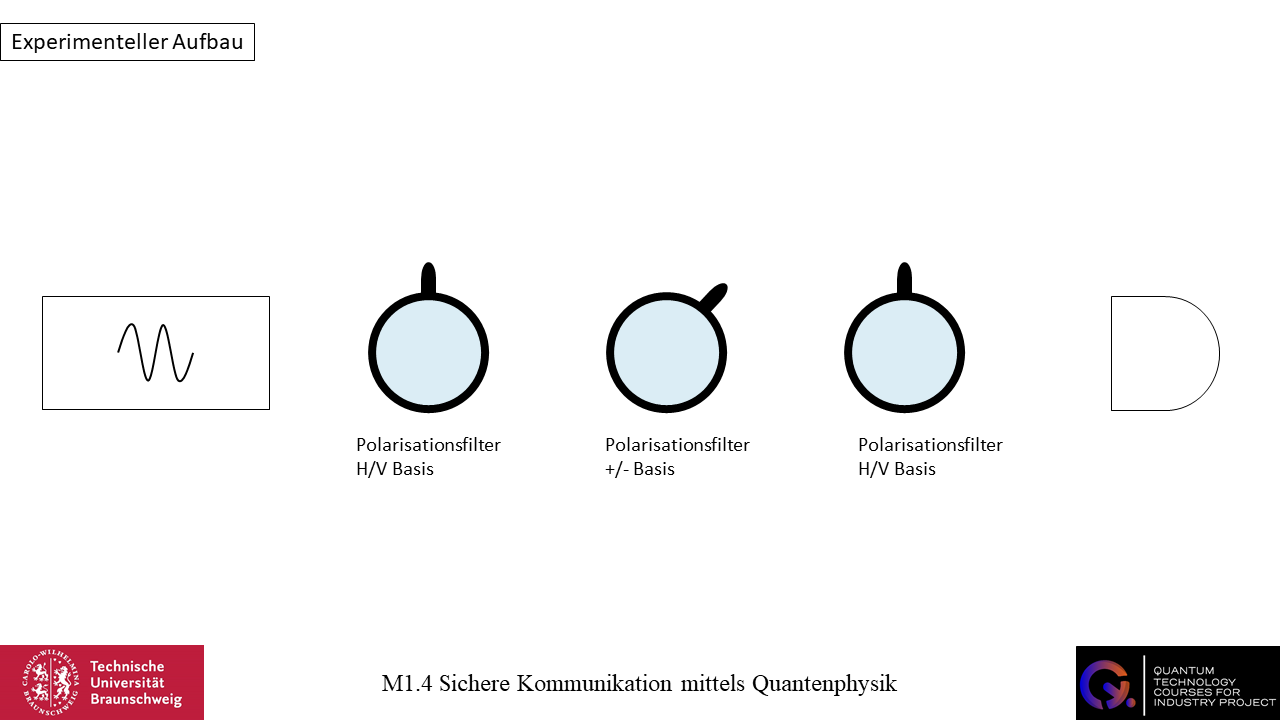
Die Abbildung zeigt einen experimentellen Aufbau, der aus drei Polarisationsfiltern, einem Einzelphotonenemitter und einem Detektor besteht. Beschreibe die unterschiedlichen Szenarien die auftreten können und erkläre, warum die Wahrscheinlichkeit, ein Photon zu detektieren, 12,5% beträgt.

Erarbeite zwei mögliche Szenarien in denen eine andere Lauscherin, Evelyn, zwischen Eve und Bob platziert ist, aber nichts von der Existenz von Eve weiß. Gibt es die Möglichkeit, dass Bob ein richtiges Bit an Information bekommt, obwohl Eve eine andere Basis als Alice und Bob benutzt? Und was bedeutet dies für den Erfolg von Evelyn’s Lauschangriff?

Weiterführende Informationen & Literatur

BB84 Protokoll:

Bennett, C.H. & Brassard, G. (1984). Quantum Cryptography: Public Key Distribution And Coin Tossing. International Conference on Computers, Systems & Signal Processing, December 10-12. Bangalore India. pp. 175-179.

Mullins, J. (2002). Making Unbreakable Code: The quantum properties of photons could make encrypted messages absolutely secure. IEEE Spectrum. pp. 40-45.

Müller, R. & Greinert, F. (2023). Quantentechnologien: Für Ingenieure. De Gruyter.

Scully, M.O., Englert, B.-G. & Walther, H. (1991). Quantum optical tests of complementarity. Nature, Vol. 351. pp. 111-116.

Quiz